Implementation of Wildcard Matching for String

Finally, I got an internship in iOS development. It’s my first time getting involved in production environments, which is quite challenging but helpful. My mentor’s first task for me is to re-implement a wildcard matching mechanism for a view router component. Although the task shouldn’t be hard for experienced developers, it’s still a little bit tough for me. It took me about a week to get through.

Background

As for most business, mobile apps are just another front-end, it’s necessary to maintain consistency between views of apps and pages of other front-ends (for example, the websites). Therefore, my co-workers built a simple routing component as a CocoaPods package to route any URLs passed from external to the corresponding ViewController in the iOS app.

Existing Implementation

By the original implementation, a trie tree is built to record registered path rules and answer URL path queries. Path rules are split up into rule components and converted into nodes of the tree.

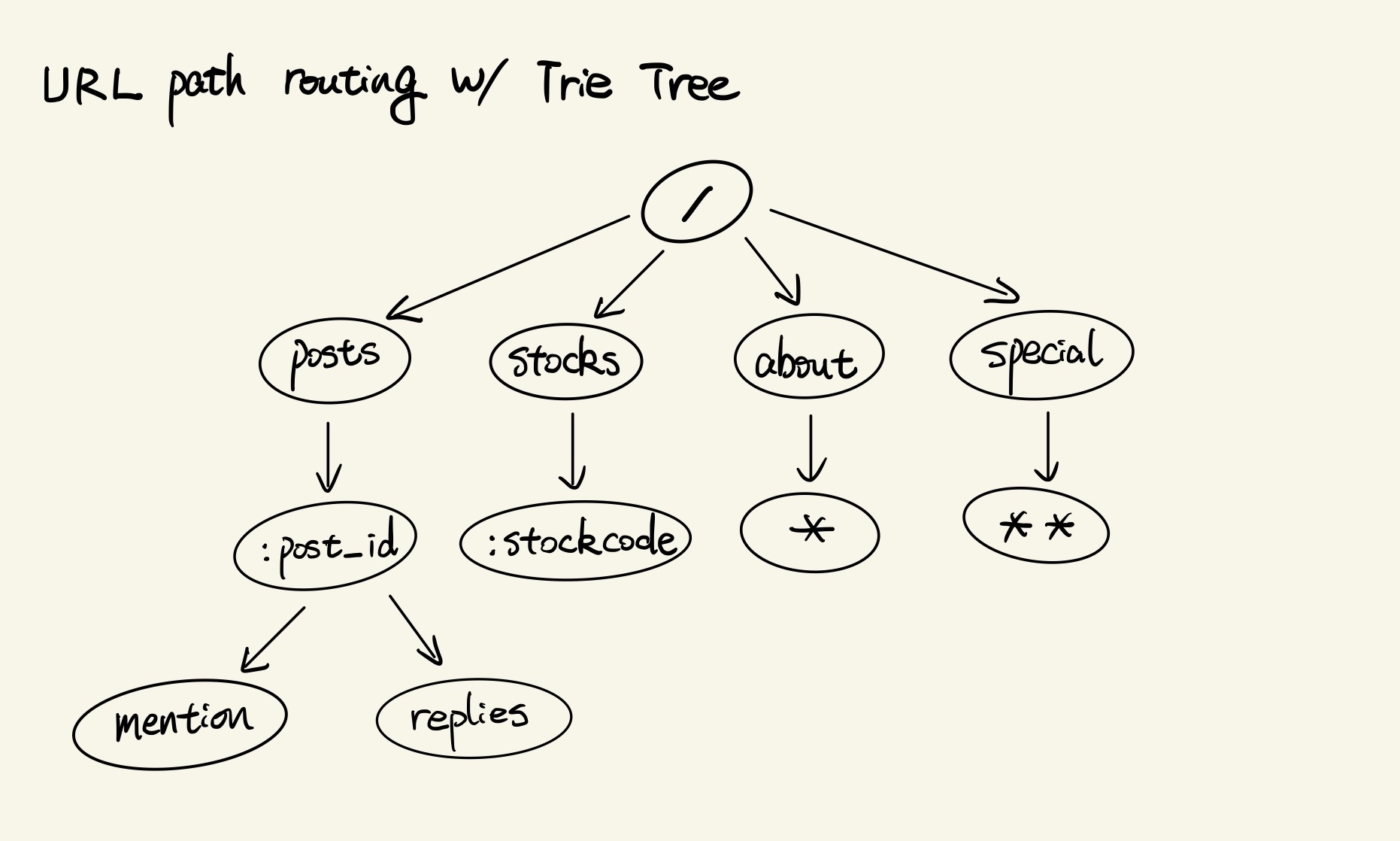
It defines 5 types of rule components defined by the package:

• Constant: plain text, match path components with the same string contents.
• Placeholder: extract contents of corresponding path components, return placeholder names and extracted contents as a dictionary back to callers.
• Pattern: patterns with * wildcards to match any possible path components.
• Anything: single * wildcard node to match a single path component.
• Catchall: single ** wildcard node to match zero or more levels of path components.

Matching mechanism of Pattern nodes from the original implementation has issues when dealing with rule components containing more than one wildcard. It divides any pattern string into two parts by the star character, then uses two internal methods of Swift String, hasPrefix(_:) and hasSuffix(_:), to validate the URL path components passed in. It is an easy and straightforward implementation but cannot handle patterns with multiple stars.

Goal

To fix the problem and improve the package, there’re two things I need to do:

1. Re-implement the matching mechanism of Pattern nodes to make them capable of processing patterns with multiple star wildcards.
2. After that, retire the original Anything nodes, as the new Pattern nodes can also be used as a single star component.

Although Swift has built-in regular expression supports, we won’t use that. Our needs are not that complex as regular expressions, using regular expressions could introduce more problems when dealing with other special characters. Besides that, it’s a chance for me to learn algorithms by practising.

Solution

Fortunately, our task is very similar to a LeetCode problem, which means lots of solutions are available from LeetCode as references for me to research. Comparing to the LeetCode problem, our need is even easier, as we don’t have the question mark rule to match any single character.

To implement the mechanism we need, two algorithms called Dynamic Programming and Memoization can be applied. Well, to be honest, I don’t exactly understand the theory of them. (As we all know, Wikipedia is available, but usually, their pages of mathematic theories are not written for normal newbies.) However, there’re other readable explanations for us to solve this specific case.

For this problem, create a (pattern.count + 1) × (string.count + 1) size table, the additional row and column are Start points for both pattern and string:

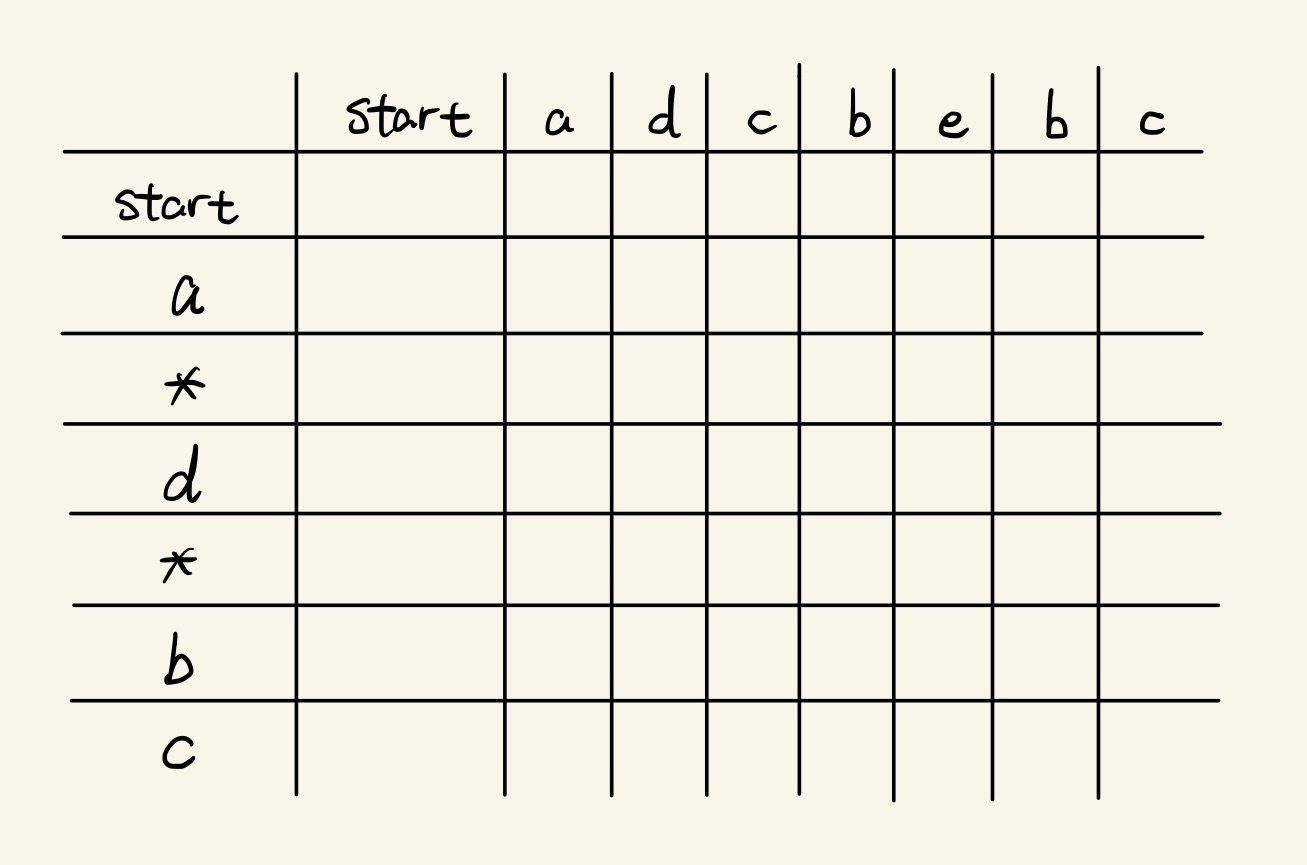
In code, it’s represented by a 2D array as dp[row][column].

⚠️ Values of row and column are always bigger than the corresponding index of pattern and string by 1.

Splitting the problem into steps, we need to match string to pattern by each character. We use each cell of the table to represent the matching result of its top-left part. For example, if dp[3][2] == true, it means the first 2 characters of the target string can match to the first 3 characters of the pattern. Based on this assumption, if the 3rd character of the target string can match to the 4th character of the pattern, we can then get dp[4][3] == true. Abstracting that, we can get our Rule #1:

if: 
    dp[row][column] == true && 
    pattern[row] == string[column]
then: 
    dp[row + 1][column + 1] = true

It can be simplified as:

# RULE 1
if: 
    pattern[row] == string[column]
then: 
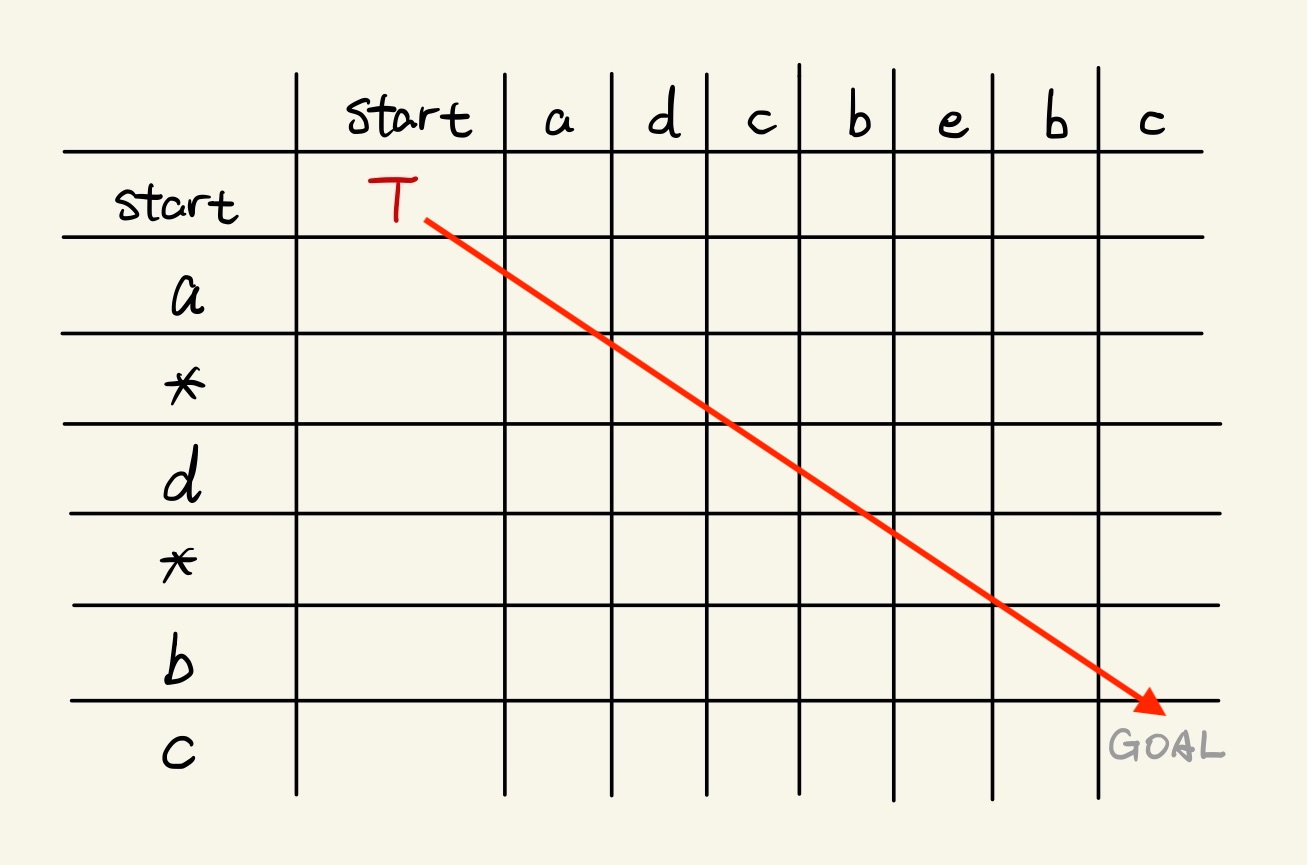
    dp[row + 1][column + 1] = dp[row][column]

Besides that, an empty string can always match to an empty pattern, so there should be dp[0][0] == true. Because it’s about the startpoint, we identify it as Rule #0:

# RULE 0
always:
    dp[0][0] == true

Reflecting Rule #0 to the table, our starting point is the most top-left cell, and our goal should be the most bottom-right cell. By default, each cell of the table is false. To reach the goal, we need to traverse each cell of the table to flip matchable ones, from left to right, top to bottom.

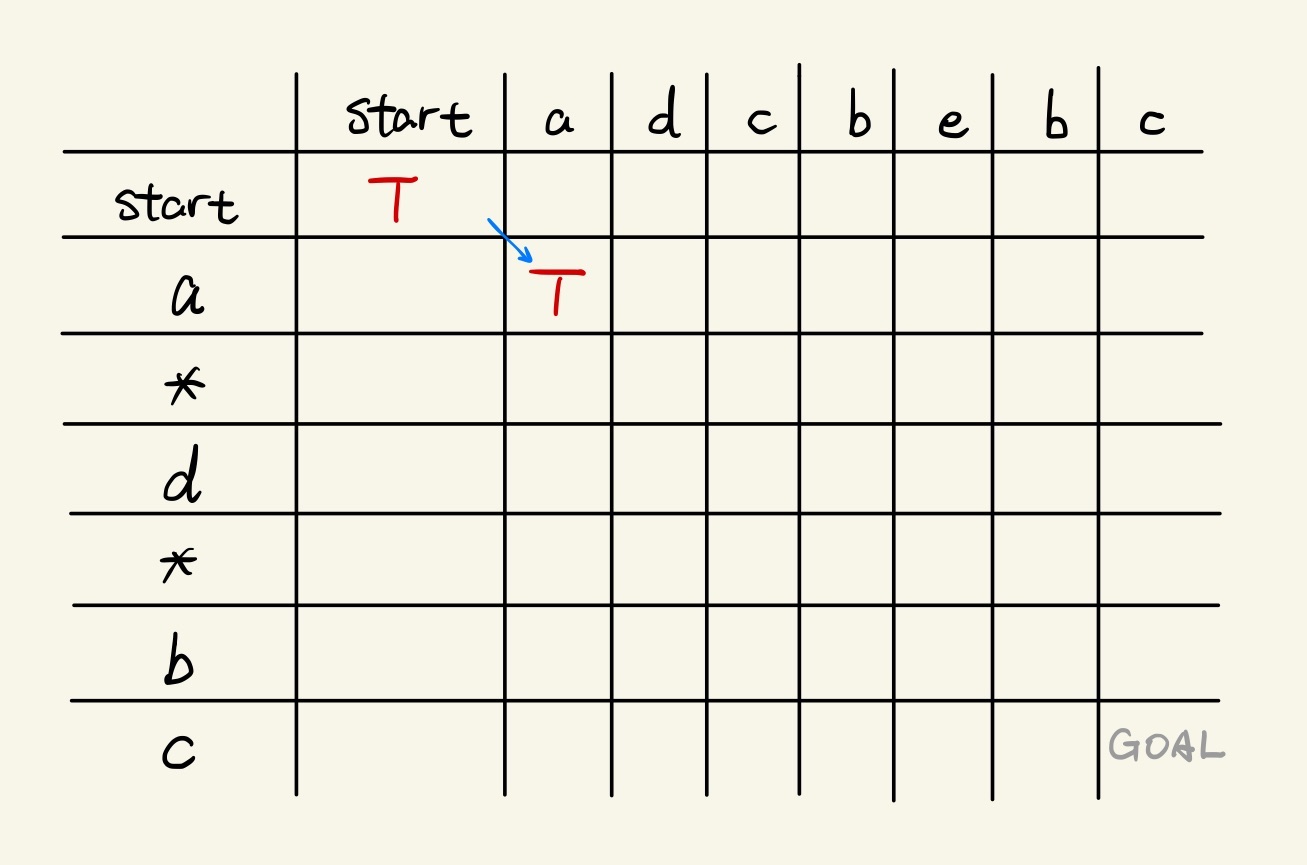
Representing Rule #1 to the table, when the current row can match to the current column, we can copy the true from the original cell to the bottom-right cell of it:

After this, we then encounter a star. For star, because it can match any characters (even zero character), we can copy the true from dp[1][1] to the bottom cell of it first, then all cells right of it in the row can be flipped as a star can be matched until the end of the string:

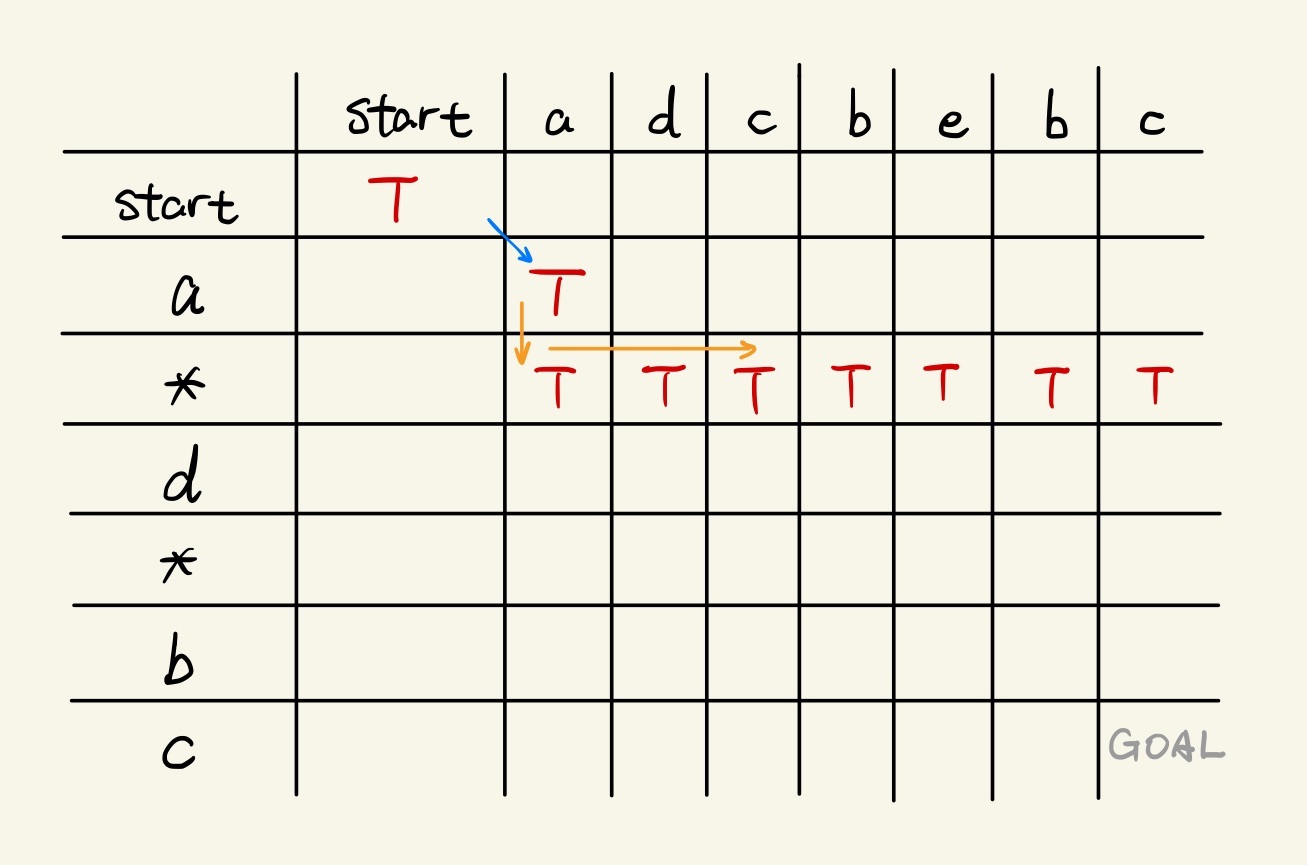
Convert our process to Rule #2, it should be:

if: 
    pattern[row - 1] == "*" &&
    dp[row - 1][column] == true &&
    n >= column
then: 
    dp[row][n] = true

It can be simplified as:

# RULE 2
if: 
    pattern[row - 1] == "*"
then: 
    dp[row][n] = dp[row - 1][n] || dp[row][n - 1]

⚠️ This expression could cause index out of boundary in code if n == 0, we’ll handle that in the final solution.

Applying all three rules above, we can finally get the table like this:

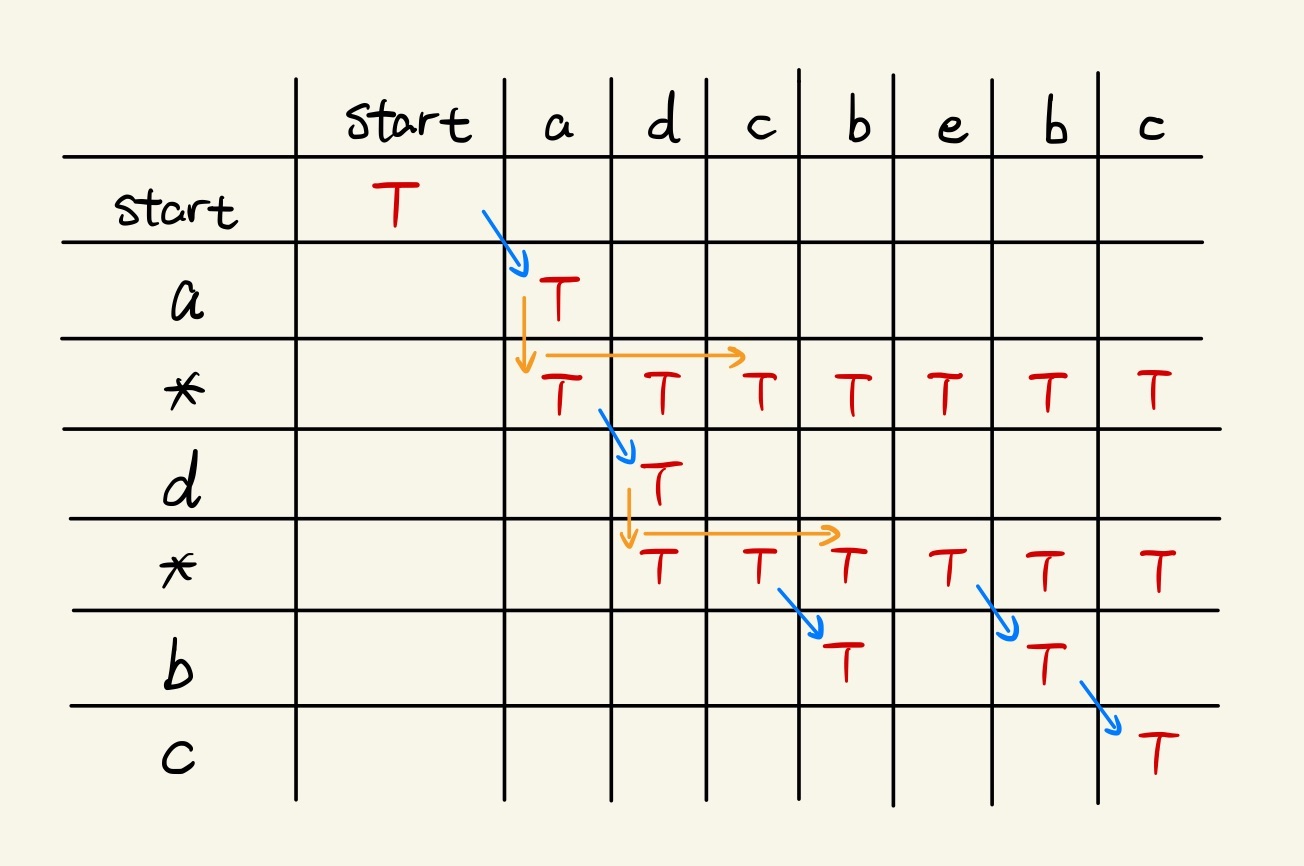
To transform our methodology into code, few points need to be considered:

• Because pattern of empty cannot be matched to any non-empty string, the first row can only have its first cell as true. Therefore, we don’t need to traverse the first row. We can simply set the initial cell as true and then move to dp[1].
• As the previous note said, the current expression of Rule #2 could cause index out of boundary. Hence we need to add an additional if case to check if the current pointing column is 0.

With all these factors considered, we can get the code below:

extension String {

    func match(pattern: String) -> Bool {
        // create a table to log the DP solution
        let height = pattern.count + 1
        let width = count + 1
        var dp = [[Bool]](repeating: [Bool](repeating: false, count: width), count: height)
        // set table start point
        dp[0][0] = true

        // scan each tile
        var pIndex = pattern.startIndex
        for hPointer in 1..<height {
            let isWildcard = pattern[pIndex] == "*"
            var sIndex = startIndex
            for wPointer in 0..<width {
                if wPointer == 0 {
                    if isWildcard {
                        // RULE 2 when in first column
                        dp[hPointer][wPointer] = dp[hPointer - 1][wPointer]
                    }
                } else {
                    if isWildcard {
                        // RULE 2
                        dp[hPointer][wPointer] = dp[hPointer - 1][wPointer] || dp[hPointer][wPointer - 1]
                    } else if pattern[pIndex] == self[sIndex] {
                        // RULE 1
                        dp[hPointer][wPointer] = dp[hPointer - 1][wPointer - 1]
                    }
                    sIndex = index(after: sIndex)
                }
            }
            pIndex = pattern.index(after: pIndex)
        }
        return dp[height - 1][width - 1]
    }
}

Algorithm, Swift — Mar 2, 2021